Can you solve these calculus problems for Pi Day?

March 14, or 3.14 in the U.S., marks Pi Day, an annual celebration of one of the world’s most famous icons of nerd culture: the irrational number pi. Founded in 1988 in San Francisco by physicist Larry Shaw, this date was selected because of the numerical date (3.14). In a bid to put the pi back in Pi Day in the midst of the coronavirus crisis, below are some math problems involving pi. National Pi Day is not complete without math problems so let’s get to the glavin!

I came across a very interesting article last January in Parade Magazine and there’s a column called “Ask Marilyn”. In that old article, she posed a really challenging multivariable calculus problem and I would like to show it to you. You’ll solve this problem using triple integrals in cylindrical coordinates.

Here’s the problem that appeared in Parade Magazine:

“You have a solid sphere (shown below) and bore a perfect hole right through the center of it. This leaves a cylindrical shell that is 6 inches long and that’s the only piece of data you know. What is the volume of the remainder of the sphere after you’ve thrown away the part that you drilled?”

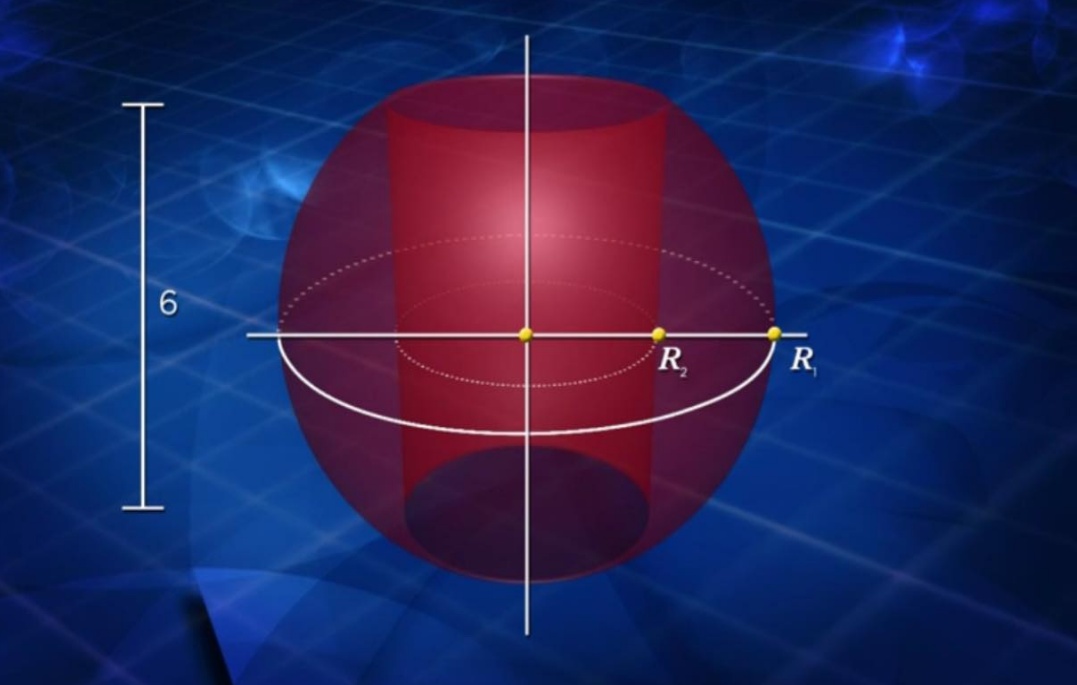
What is interesting about this problem is you’re never given the radius of the sphere nor the radius of the cylindrical hole that you drilled through the middle. The only datum you have is that it’s 6 inches long. And yet we’ll be able to calculate the remaining volume of that sphere using triple integrals in cylindrical coordinates that are especially useful for representing cylindrical surfaces and surfaces of revolution. You have to think of the number pi when solving this problem. Why? Because no matter how big or small a pi is—from the size of our solar system all the way down to subatomic particles—the ratio of a circle’s circumference to its diameter is equal to pi. In the same vein, the volume of this cylindrical sphere is the same regardless of its size. And while you can solve this using the washer method, I think the easiest way to calculate the volume is by using triple integrals in cylindrical coordinates shown below:

(By the way, the conversion formulas are similar to the conversion formulas between polar coordinates and Cartesian coordinates.)

For the second math problem involving pi (shown below), the following integral was posted by undergraduate math students somewhere in China. One of their math professors posted this calculus problem in the dining hall and they had to evaluate the following definite integrals in order to access the WiFi. You’ll solve this problem using only pencil and paper and without the aid of a graphing calculator. This math problem is quite basic and straightforward if you know a few tricks in analytical geometry and integration by parts.

Good luck!

Anthony Quilon